百科生活 投稿
关于【关于计算流体力学介绍】,计算流体力学导论,今天小编给您分享一下,如果对您有所帮助别忘了关注本站哦。
- 内容导航:
- 1、一文带你了解计算流体力学CFD及其应用领域
- 2、关于计算流体力学介绍
1、一文带你了解计算流体力学CFD及其应用领域
计算流体力学的发展
计算流体动力学 (Computational Fluid Dynamics) 简写为CFD,经过半个世纪的迅猛发展,这门学科已经是相当的成熟了,一个重要的标志就是近几十年来,各种CFD通用软件的陆续出现,成为商品化软件,服务于传统的流体力学和流体工程领域,如航空、航天、船舶、水利等。随着CFD通用软件的性能日益完善,应用的范围也不断的扩大,在化工、冶金、建筑、环境等相关领域中也被广泛应用。
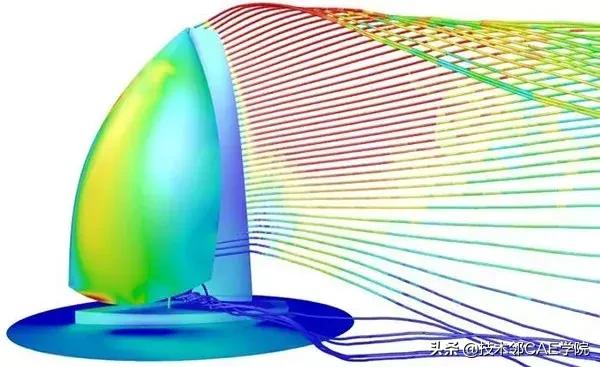
现代流体力学研究方法包括理论分析,数值计算和实验研究三个方面。这些方法针对不同的角度进行研究,相互补充。理论分析研究能够表述参数影响形式,为数值计算和实验研究提供了有效的指导;试验是认识客观现实的有效手段,验证理论分析和数值计算的正确性;计算流体力学通过提供模拟真实流动的经济手段补充理论及试验的空缺。
更重要的是,计算流体力学提供了廉价的模拟、设计和优化的工具,以及提供了分析三维复杂流动的工具。在复杂的情况下,测量往往是很困难的,甚至是不可能的,而计算流体力学则能方便的提供全部流场范围的详细信息。与试验相比,计算流体力学具有对于参数没有什么限制,费用少,流场无干扰的特点。出于计算流体力学如此的优点,我们选择它来进行模拟计算。简单来说,计算流体力学所扮演的角色是:通过直观地显示计算结果,对流动结构进行仔细的研究。
计算流体力学在数值研究大体上沿两个方向发展,一个是在简单的几何外形下,通过数值方法来发现一些基本的物理规律和现象,或者发展更好的计算方法;另一个则为解决工程实际需要,直接通过数值模拟进行预测,为工程设计提供依据。理论的预测出自于数学模型的结果,而不是出自于一个实际的物理模型的结果。计算流体力学是多领域交叉的学科,涉及计算机科学、流体力学、偏微分方程的数学理论、计算几何、数值分析等,这些学科的交叉融合,相互促进和支持,推动了学科的深入发展。

CFD方法是对流场的控制方程用计算数学的方法,将其离散到一系列网格节点上求其离散的数值解的一种方法,控制所有流体流动的基本定律是质量守恒定律、动量守恒定律和能量守恒定律。由它们分别导出连续性方程、动量方程(N-S方程)和能量方程。应用CFD方法进行平台内部空气流场模拟计算时,首先需要选择或者建立过程的基本方程和理论模型,依据的基本原理是流体力学、热力学、传热传质等平衡或守恒定律。
由基本原理出发可以建立质量、动量、能量、湍流特性等守恒方程组,如连续性方程、扩散方程等。这些方程构成的非线性偏微分方程组,不能用经典的解析法,只能用数值方法求解。
求解上述方程必须首先给定模型的几何形状和尺寸,确定计算区域并给出恰当的进出口,壁面以及自由面的边界条件。而且还需要适宜的数学模型及包括相应的初值在内的,过程方程的完整数学描述。
求解的数值方法主要有,有限差分法 (FDM) 和有限元 (FEM) 以及有限分析法 (FAM),应用这些方法可以将计算域离散为一系列的网格并建立离散方程组,离散方程的求解是由一组给定的猜测值出发迭代推进,直至满足收敛标准。常用的迭代方法有Gauss-Seidel迭代法、TDMA方法、SIP法及LSORC法等。利用上述差分方程及求解方法,可以编写计算程序或选用现有的软件实施过程的CFD模拟。

计算流体力学应用领域
近十多年来,CFD有了很大的发展,替代了经典流体力学中的一些近似计算法和图解法,过去的一些典型教学实验,如Reynolds实验,现在完全可以借助CFD手段在计算机上实现。
所有涉及流体流动、热交换、分子输运等现象的问题,几乎都可以通过计算流体力学的方法进行分析和模拟。CFD不仅作为一个研究工具,而且还作为设计工具在水利工程、土木工程、环境工程、食品工程、海洋结构工程、工业制造等流域发挥作用。典型的应用场合及相关的工程问题包括:
1
航空工程
CFD在航空和国防工业中的应用经历了一个长期的发展过程,取得了令人瞩目的成绩。在激烈的竞争环境中,CFD在改进飞行设计中起到了关键性的作用。实际上,很多工程师已将CFD和空气动力学结合起来用于诸如飞机机翼升力的计算。随着CFD计算技术和计算机能力的提高,其使用更为简便,人们在计算升力之外,其应用范围已经得到很大拓展。今天,CFD正用于求解很多困难的实际问题,而这些问题用过去的计算工具是难以分析或求解的。

2
汽车工程
现在,汽车工程师们正在依靠更多的模拟技术,将提出的新车设计概念付诸实施。计算机辅助工程已经处于革新汽车内部系统的技术前沿,可以更好地全面提升驾驶体验,改善驾破员和乘客的舒适性和安全性,并且进一步降低油耗。计算流体力学长期以来一直是汽车设计和制造中的一个基本要素,除了航空航天工业外,汽车工业在研究制造中也大量使用了CFD技术。因此,作为工程模拟工具,即使面对最困难的挑战,CFD仍然在许多工业领域中得到很好的应用。
3
生物科学工程
医学研究者现在依靠模拟工具帮助预测人体中血液循环流动状态,数值模拟能够提供实验难以得到的有价值的信息,而且CFD还可以对很多流体动力学参数进行研究。同时,CFD在制药工业也有广泛的应用。
4
化学和采矿工程
很多世界必需品源于化学工业和采矿业,这些工业通过物理或化学方法加工原材料,消耗大量的热能和电能,为食品、保健品以其先进的计算技术设备和生物技术设备提供初级产品。面对不断加剧的竞争,这些工业面临的主要挑战是既要满足当前世界性的需求,同时对未来发展不造成损害,这就要求生产过程更高效、更安全以及更少污染物的排放。
5
民用和环境工程
政府、研究机构以及企业正在寻求途径满足环境保护法,在维持一定生产水平、满足市场不断增加需要的同时,保证减少环境污染。在很多时候,CFD模拟已经成为解决环境问题的核心技术。
6
能源工程
在不断竞争的能源市场中,设备制造商们转向CFD寻求技术支持,以便更好地了解和提升能源工业中的设备和工艺。尽管传统的发电方式仍在广泛使用,但已经出现了具有潜力的可再生能源,如风力发电。为使投资得到最大回报,CFD已经被用于风力发电涡轮叶片的优化设计当中,使之在不同的来风条件下能产生恒定的功率。通过CFD的风能资源评估,工程师可以更好地研究风力发电站的经济性,正确的模拟结果可以减少投资风险。
7
体育
随着体育水平的不断提高,特别是在奥运赛场上,运动员的水平都在伯仲之间,体育比赛的胜负差距非常微小,为了在比赛中获得胜利,不得不为提高器材的性能投入大量的资金。体育器材的流体动力性能越来越重要,越来越多的优秀运动员、运动队以及体育设备制造商们,都在努力从先进的流体模型中获取比赛空气动力的有利条件,越来越多的体育器材外形的研究成果逐渐为人们所认可。同时,CFD不仅可以研究体育运动器械等硬件设备,还可以对运动员的运动技巧进行分析,针对不同运动员的自身条件,通过计算分析,制定更为科学量化的竞技动作和训练内容。
来源:工程事
-END-
2、关于计算流体力学介绍
[拼音]:jisuan liuti lixue
[外文]:computational fluid dynamics
用电子计算机和离散化的数值方法对流体力学问题进行数值模拟和分析的一个新分支。
简史流体力学和其他学科一样,是通过理论分析和实验研究两种手段发展起来的。很早就已有理论流体力学和实验流体力学两大分支。理论分析是用数学方法求出问题的定量结果。但能用这种方法求出结果的问题毕竟是少数,计算流体力学正是为弥补分析方法的不足而发展起来的。
早在20世纪初,理查德就已提出用数值方法来解流体力学问题的思想。但是由于这种问题本身的复杂性和当时计算工具的落后,这一思想并未引起人们重视。自从40年代中期电子计算机问世以来,用电子计算机进行数值模拟和计算才成为现实。1963年美国的F.H.哈洛和J.E.弗罗姆用当时的IBM7090计算机,成功地解决了二维长方形柱体的绕流问题并给出尾流涡街的形成和演变过程,受到普遍重视。1965年,哈洛和弗罗姆发表“流体动力学的计算机实验”一文,对计算机在流体力学中的巨大作用作了引人注目的介绍。从此,人们把60年代中期看成是计算流体力学兴起的标志。
计算流体力学的历史虽然不长,但已广泛深入到流体力学的各个领域,相应地也形成了各种不同的数值解法。 就目前情况看, 主要是有限差分方法和有限元法。有限差分方法在流体力学中已得到广泛应用。而有限元法是从求解固体力学问题发展起来的。近年来在处理低速流体问题中,已有相当多的应用,而且还在迅速发展中。
流体力学基本方程为了说明计算流体力学主要方法,需先了解流体力学运动的基本方程的性质和分类。流体力学的基本方程是在19 世纪上半叶由C.-L.-M.-H.纳维和G.G.斯托克斯等人建立的,称为纳维-斯托克斯方程,简称N-S方程。二维非定常不可压缩流体的N-S方程为:
式中u、v为沿着x、y方向上的速度分量;t为时间;p为压力;ρ为密度;ν为运动粘性系数。在不同条件下,N-S方程的数学性质也不一样。
(1)N-S方程描述粘性流体随时间而变的非定常运动。时间项和方程右边的高阶导数项决定方程的性质。它同二维热传导方程类似,属于抛物型方程。
(2)粘性流体的定常运动是将原方程中的时间项省去。此时N-S方程的性质,取决于它的高阶导数项,和拉普拉斯方程一样,为椭圆型方程。
(3)无粘流的欧拉方程是将 N-S方程的右边粘性项略去而得。它也适用于可压缩流体。从形式上不容易判断欧拉方程的性质。因多数无粘流动皆为无旋流动,故如将欧拉方程改用速度势嗞表示, 则二维定常可压缩气流的方程为:
(c2-u2)嗞xx-2uv嗞xy+(c2-v2)嗞yy=0,
式中c为声速。此式是二阶偏微分方程
A嗞xx+2B嗞xy+C嗞yy+D嗞x+E嗞y=0
的一般形式, 其性质要看B2-AC0而定。 在超声速区,B2-AC>0,即u2+v2>c2,上式类似于波动方程,为双曲型;在亚声速区,B2-AC<0,即u2+v2<c2,上式便与拉普拉斯方程相同,为椭圆型。总之,流体力学的运动方程是极其复杂的非线性偏微分方程,具有各种不同的类型,而且往往还是混合型的。要全面描述流体的运动,还必须同时考虑其他方程,如连续性方程、能量方程和状态方程等。所以计算流体力学在很大程度上就是针对不同性质的偏微分方程采用和发展相应的数值解方法。
低速无粘流动数值解在无旋条件下,低速流动的速度势满足拉普拉斯方程或泊松方程。很多平面问题利用复变函数和保角映射可以求得解析解,这是经典流体力学的重要内容。但对几何形状比较复杂的物体,必须用下述的数值解法。
(1)迭代解法 这是用逐步近似求解联立方程的方法,也是椭圆型微分方程的主要数值解法。此法程序简单,存储量与运算量均比较小,一般先假定一组初值,然后求每个网点上的新值。以五点格式为例,网点上的新值是邻近四点初值的平均。新值求出后,旧值还要保留,以便计算其他各点的新值。这种简单迭代收敛很慢,现已很少使用。但若稍加改进,用算出的新值冲掉旧值,并引进一个松弛因子,以加速收敛,将算出来的新值与原来的旧值加权平均,就成为50年代发展起来的逐次超松弛法。
(2)时间相关法 这是用非定常方程求解定常问题的方法,常用于求解N-S方程和欧拉方程等。虽然用的是非定常方程,但所解的并不是非定常问题。根据给定的初始条件以及随时间改变的约束条件,非定常问题是研究流动随时间的演变过程。这种非定常行为和给出的初值很有关系。然而时间相关法的初值,原则上是随意选取的,只是须满足定常问题所规定的边界条件。在求解过程中,流动随时间的变化并不代表真实的物理过程。当时间足够长后,未知函数值逐步与时间无关,便渐近趋于定常解。所以时间相关法实际上也是一种迭代法,时间变量只不过是用来记录迭代的次数而已。
(3)交替方向隐式法 流体力学的应用问题,往往是二维和三维的空间问题。由于稳定性的要求,时间步长受维数的限制,维数愈高,要求时间步长愈小,计算工作量也愈大。50年代中期D.W.裴斯曼和J.道格拉斯等人提出所谓交替方向隐式法,以加快计算速度。如在二维非定常方程中,第一步先对x的导数用隐式差分,而y方向的导数则用前一个的数值。第二步对y的导数用隐式差分,x方向的导数则用第一步算出来的数值。这一方法的优点是稳定性好,有足够的二阶精度,所产生的差分方程是三对角矩阵方程,便于求解。
(4)有限基本解法 解位势流动的一种数值方法。航空工业中的低速飞机设计采用位势理论计算各种气动力参数,就是求解二维或三维拉普拉斯方程。在经典流体力学中,用基本解的叠加来解拉普拉斯方程的做法是很成功的。这种方法的要点是,用源、汇、偶极子的分布代替机翼和机身对流场的影响。它们的强度由边界条件确定,结果需要求解积分方程。对一些简单情况可以求解,对一般情况则比较困难。高速电子计算机的出现使这种积分方程的数值解法也有了突破。其主要思想是把积分方程离散化,积分方程代表源、汇等奇点在空间连续分布的总和。例如,若把机翼和机身表面,分割成若干个小单元,每个单元上的奇点强度取平均值。把这些奇点的总和叠加起来,就得出流场总的效应。因此,它用有限项的求和来代替积分,而最后要解的是一组代数方程。由于基本解都是具有奇点的函数,所以这种方法又称为有限奇点法或鳞片法。(见有限基本解法)
跨声速流动数值解跨声速流动的流场是既有亚声速区又有超声速区的一种混合流场。在不考虑粘性影响和小扰动的情况下,定常二维速度势方程是混合型的,即V嗞xx+嗞yy=0,式中V是来流马赫数Ma∞与嗞x的复杂函数。V>0是亚声速区(椭圆型),而V<0为超声速区(双曲型)。美国的E.M.穆曼和J.D.科尔在1971年首先采用混合差分格式,并运用松弛法成功地解出定常小扰动速度势方程。混合差分格式就是在亚声速区用中心差分格式,所有邻近网点上的条件都会影响计算点,而在超声速区,则用迎风格式,因为上游迎风网点正好是双曲型波动方程的依赖区。(见跨声速流数值计算)
超声速流动数值解在超声速流动中,主要问题是如何处理激波。用数值方法处理超声速流场中的激波现有两种方法。一是激波捕捉法,另一是激波装配法。激波捕捉法对激波本身并不需作任何特殊处理,只是在计算公式中,直接或间接地引进“粘性”项,自动算出激波的位置和强度,以“捕捉”激波。其中又有所谓人工粘性和格式粘性两种方法。 人工粘性方法是J.von诺伊曼和R.D.里希特迈尔于1950年首先提出的,它是以真实粘性流体的物理理论为基础的一种自动处理激波近似方法。该法是在激波层内,人为地加入粘性项,使激波间断变成光滑的过渡区。近年来,在超声速流动中得到广泛的应用。格式粘性是通过某种差分格式间接地引入粘性项拉克斯格式。 拉克斯-文德霍夫格式和麦克马克格式都具有类似的效果。激波装配法是把激波仍当作间断面来处理,激波前后要满足激波跳跃条件。但是在普通坐标中,它的实现很困难。一般采用坐标变换,使激波位置(此时是未知的)和一个坐标轴重合,然后把激波看作内边界。这种处理是比较精确的,但也是很麻烦和不方便的。最好的办法是把激波捕捉法和激波装配法结合起来。例如在流场外围的离体激波用激波装配法,在流场内的激波用激波捕捉法。(见超声速无粘绕流数值解)
粘性流动数值解法可参见纳维-斯托克斯方程数值解、边界层方程数值解法和湍流数值计算等。
- 参考书目
- 朱幼兰等著:《初边值问题差分方法及绕流》,科学出版社,北京,1980。
- P.J.罗奇著,钟锡昌、刘学宗译:《计算流体力学》,科学出版社,北京,1983年。
- P.J.Roache,Computation Fluid Dynamics,Hermosa Pub., Albuquerque,1972.
本文关键词:计算流体力学是什么,关于计算流体力学介绍的书籍,关于计算流体力学介绍正确的是,计算流体力学综述,计算流体力学简介。这就是关于《关于计算流体力学介绍,计算流体力学导论(一文带你了解计算流体力学CFD及其应用领域)》的所有内容,希望对您能有所帮助!
- 最近发表