百科生活 投稿
关于【概率论常见概率分布表】,今天涌涌小编给您分享一下,如果对您有所帮助别忘了关注本站哦。
- 内容导航:
- 1、概率论常见概率分布表:常用的连续概率分布汇总
- 2、概率论常见概率分布表,数据科学家都应该知道这5个概率分布
1、概率论常见概率分布表:常用的连续概率分布汇总
来源:Deephub IMBA
本文约1800字,建议阅读5分钟
本文为你详细介绍常用的连续概率分布。
在数学中,连续型随机变量的概率密度函数(在不至于混淆时可以简称为密度函数)是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。
均匀分布
在概率论和统计学中,均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为U(a,b)。
CDF曲线是
累积分布函数(Cumulative Distribution Function),又叫分布函数,是概率密度函数的积分,能完整描述一个实随机变量X的概率分布。一般以大写CDF标记,,与概率密度函数probability density function(小写pdf)相对.
正态分布
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由棣莫弗(Abraham de Moivre)在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。
P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
正态性检验包括Shapiro-Wilk W检验、Anderson-Darling检验(AD-Test)和Kolmogorov-Smirnov检验。
如果log(x)是正态分布,x是对数正态分布
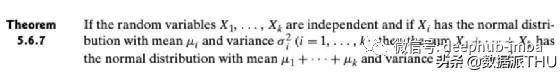
指数分布
在概率理论和统计学中,指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。这是伽马分布的一个特殊情况。它是几何分布的连续模拟,它具有无记忆的关键性质。除了用于分析泊松过程外,还可以在其他各种环境中找到。
指数分布与分布指数族的分类不同,后者是包含指数分布作为其成员之一的大类概率分布,也包括正态分布,二项分布,伽马分布,泊松分布等等。
可以使用指数分布对不同事件发生之间所花费的时间进行建模。比如:包括生存分析(设备/机器的预期寿命),以及指定时间段内的指定数量的默认值。在金融领域,它常被用来衡量金融资产组合下一次违约的可能性。
指数函数的一个重要特征是无记忆性(Memoryless Property,又称遗失记忆性)。这表示如果一个随机变量呈指数分布,当s,t>0时有P(T>t+s|T>t)=P(T>s)。即,如果T是某一元件的寿命,已知元件使用了t小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等。在连续概率分布中,只有指数随机变量具有这种性质。
t分布
t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。
如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
当²未知时,t分布可以用来推断总体均值。当自由度为无穷大时,t分布=正态分布。
伽玛分布
伽玛分布(Gamma Distribution)是统计学的一种连续概率函数,是概率统计中一种非常重要的分布。“指数分布”和“χ2分布”都是伽马分布的特例。泊松过程中连续出现之间的时间具有指数分布。
对时间序列进行建模预测接下来发生 n 个事件时就会出现伽马分布。它在机器学习中被当作“共轭先验”使用。
Gamma 函数
当形状参数α=1时,伽马分布就是参数为γ的指数分布,X~Exp(γ)。
当α=n/2,β=1/2时,伽马分布就是自由度为n的卡方分布,X^2(n)。
贝塔分布
贝塔分布(Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。在概率论中,贝塔分布,也称Β分布,是指一组定义在(0,1) 区间的连续概率分布。
贝塔分布最适合表示概率的概率分布 - 也就是说,当我们不知道概率是什么时,它表示概率的所有可能值。
beta函数
F 分布
F分布是1924年英国统计学家Ronald.A.Fisher爵士提出,并以其姓氏的第一个字母命名的。它是两个服从卡方分布的独立随机变量各除以其自由度后的比值的抽样分布,是一种非对称分布,且位置不可互换。F分布有着广泛的应用,如在方差分析、回归方程的显著性检验中都有着重要的地位。
F 分布经常作为检验统计量的零分布出现,尤其是在与方差相等和方差分析 (ANOVA) 相关的 F 检验中。
韦布尔分布
韦布尔分布,即韦伯分布(Weibull distribution),又称韦氏分布或威布尔分布,是可靠性分析和寿命检验的理论基础。
韦氏分布可以模拟随时间增加(或减少)的故障率,而当磨损率或故障率(例如,故障率)恒定时,指数分布是合适的。所以韦氏分布在可靠性工程中被广泛应用,尤其适用于机电类产品的磨损累计失效的分布形式。由于它可以利用概率值很容易地推断出它的分布参数,被广泛应用于各种寿命试验的数据处理。
2、概率论常见概率分布表,数据科学家都应该知道这5个概率分布
概率分布就像3D眼镜。它们使熟练的数据科学家能够识别完全随机变量中的模式。
在某种程度上,大多数数据科学或机器学习技能都是基于对数据概率分布的某些假设。
这使得概率知识成为统计学家构建工具箱的基础。如果你正在思考如何成为一名数据科学家,那么这是第一步。
废话少说,让我们开门见山吧!
什么是概率分布?
在概率论和统计学中,随机变量是一个可以随机取不同值的变量,比如“我看到的下一个人的身高”或“我下一个拉面碗里厨师头发的数量”。
给定一个随机变量X,我们想描述它取哪个值。更重要的是,我们想要描述变量取某个值x的可能性有多大。
例如,如果X是“我女朋友养了多少只猫”,那么这个数字可能是1,甚至可以是5或10。
当然,一个人不可能拥有负数的猫。
因此我们希望用一种明确的数学方法来表示变量X可以取的每一个可能的值,以及事件(X= x)的可能性。
为了做到这一点,我们定义了一个函数P,使得P(X = x)是变量X值为x的概率。
我们也可以用P(X < x)或者P(X > x)来代替离散值。这非常重要。
P是变量的密度函数,它表征变量的分布。
随着时间的推移,科学家们已经意识到,自然界和现实生活中的许多事物往往表现相似,变量共享一个分布,或具有相同的密度函数(或类似的函数)。
要使P成为一个实际的密度函数,需要一些条件。
- P(X =x) <= 1 对于任意值X, P(X =x)必须小于等于1
- P(X =x) >= 0 对于任意值X, P(X =x)必须大于等于0
- 对于任意值X,P(X =x) 所有值的和为1(X取任意值的概率,加起来等于1)
离散与连续随机变量分布
随机变量可以分为两组:离散随机变量和连续随机变量。
离散随机变量
离散变量有一组离散的可能值,每个值的概率都是非零的。
例如,当我们抛硬币时,如果我们说
X = " 1如果硬币是正面,0如果是反面"
P(X = 1) = P(X = 0) = 0.5
但是请注意,离散集不一定是有限的。
几何分布,事件发生的概率为p,试验k次才得到第一次成功的概率:
k可以取任何非负的正整数。
注意所有可能值的概率之和仍然是1。
连续随机变量
如果说
X =“从我头上随机拔下的一根头发的长度,以毫米为单位(没有舍入)”
X可以取哪些值?我们知道负数在这里没有任何意义。
但是,如果你说的是1毫米,而不是1.1853759……或者类似的东西,我要么怀疑你的测量技能,要么怀疑你的测量报告错误。
连续随机变量可以取给定(连续)区间内的任何值。
如果X为连续性随机变量,则用f(x)表示X的概率分布密度函数。
用P(a < X < b)表示X位于值a和b之间的概率。
为了得到X取任一指定实数a的概率,需要把X的密度函数从a积分到b。
现在您已经知道了概率分布是什么,让我们来学习一些最常见的分布!
一、伯努利概率分布伯努利分布的随机变量是最简单的随机变量之一。
它表示一个二进制事件:“这件事发生”vs“这件事没有发生”,并以值p作为唯一的参数,表示事件发生的概率。
伯努利分布的随机变量B的密度函数为:
P(B = 1) = p, P(B =0)= (1- p)
这里B=1表示事件发生了,B=0表示事件没有发生。
注意这两个概率加起来是1,因此不可能有其他值。
二、均匀概率分布均匀随机变量有两种:离散随机变量和连续随机变量。
离散均匀分布将取(有限的)一组值S,并为每个值分配1/n的概率,其中n是S中的元素数量。
这样,如果变量Y在{1,2,3}中是均匀的,那么每一个值出现的概率都是33%。
骰子就是一个非常典型的离散均匀随机变量,典型骰子有一组值{1,2,3,4,5,6},元素数量为6,每个值出现的概率是1/6。
连续均匀分布只取两个值a和b作为参数,并在它们之间的区间内为每个值分配相同的密度。
这意味着Y在一个区间(从c到d)取值的概率与它的大小相对整个区间(从b到a)的大小成正比。
因此,如果Y在a和b之间均匀分布,则
这样,如果Y是1和2之间的均匀随机变量,
P(1 < X < 2)=1, P(1 < X < 1.5) = 0.5
Python的随机包的随机方法就采样了一个在0到1之间均匀分布的连续变量。
有趣的是,可以证明,在给定均匀随机值生成器和一些微积分的情况下,可以对任何其他分布进行采样。
三、正态概率分布
正态分布变量在自然界中很常见,它们是常态,这就是这个名字的由来。
如果你把你所有的同事召集起来,测量他们的身高,或者给他们称重,然后用结果绘制一个直方图,结果很可能接近正态分布。
如果你取任意一个随机变量的样本,对这些测量值取平均值,重复这个过程很多次,这个平均值也会有一个正态分布。这个事实很重要,它被称为统计学基本定理。
正态分布变量:
- 呈对称钟形曲线, 以均值为中心(通常称为μ)。
- 可以取实空间上的所有值,正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。标准差σ决定了分布的幅度。
- 几乎无处不在
大多数情况下,如果你测量任何经验数据,并且它是对称的,一般可假设它是正态分布。
例如,掷K个骰子,然后把结果相加,就会得到正态分布。
四、对数正态分布概率分布
对数正态概率分布是正态概率分布中较少见的一类。
如果变量Y = log(X)遵循正态分布,则称变量X为对数正态分布。
在直方图中,对数正态分布是不对称的,标准差σ越大分布越不对称。
我认为对数正态分布值得一提,因为大多数以货币为基础的变量都是这样的。
如果你看与钱有关的任何变量的概率分布,比如
- 某银行最近一次转账的金额。
- 华尔街最新成交量。
- 公司特定季度收益。
它们通常不会是正态概率分布,更接近于对数正态随机变量。
(如果你能想到你在工作中遇到的任何其他对数正态变量,请在评论中发表你的看法!尤其是财务以外的事情)。
五、指数概率分布
指数概率分布也随处可见,与泊松分布概率概念紧密相连。
泊松分布直接从维基百科中剽窃而来,它是“一个事件以恒定的平均速率连续独立地发生的过程”。
这意味着,如果:
- 你有很多事情要做。
- 它们以一定的速度发生(不随时间改变)。
- 任何一个成功的事件都不应该影响另一个成功的事件。
泊松分布可能是发送到服务器的请求、发生在超市的交易、或者在某个湖中捕鱼的鸟。
想象一下频率为λ的泊松分布(比如,事件每秒发生一次)。
指数随机变量模拟事件发生后,下一个事件发生所需的时间。
有趣的是,在泊松分布中,事件可以发生在任何时间间隔内0到∞之间的任何地方(概率递减)。
这意味着无论你等待多久,事件发生的可能性都不是零。这也意味着它可能在很短的时间内发生很多次。
在课堂上,我们常开玩笑说公交车到站是泊松分布。我认为,当你给一些人发送WhatsApp消息时的响应时间也符合这个标准。
λ参数调节活动的频率。它将使事件实际发生所需的预期时间以某个值为中心。
这意味着,如果我们知道每15分钟就有一辆出租车经过我们的街区,即使理论上我们可以永远等下去,我们极有可能等不到30分钟。
数据科学中的指数概率分布
这是指数分布随机变量的密度函数:
假设你有一个变量的样本,想看看它是否可以用指数分布变量来建模。
最佳λ参数可以很容易地估计为采样值平均值的倒数。
指数变量非常适合建模任何罕见但巨大的离群值。
这是因为它们可以取任何非负的值,但以较小的值为中心,随着值的增长频率降低。
在特别是异常繁重的样本中,你可能想要估计λ中位数而不是平均值, 因为中位数对异常值更为稳健。在这一点上,你的利益可能会有所不同,所以对它持保留态度。
结论总而言之,作为数据科学家,我认为学习基础知识非常重要。
概率和统计可能不像深度学习或无监督机器学习那么浮华,但它们是数据科学的基石,更是机器学习的基石。
根据我的经验,提供具有特性的机器学习模型,而不知道他们遵循哪种分布是一个糟糕的选择。
记住指数分布和正态分布的普遍性,以及较罕见的对数正态分布也是很好的。
在训练机器学习模型时,了解它们的特性、用途和表现将扭转格局。在进行任何类型的数据分析时,将它们牢记于心通常也是有好处的!
本文关键词:概率论都有哪些分布,概率论常用分布总结,概率论分布大全,概率分布都有哪些,概率论常见概率分布表有哪些。这就是关于《概率论常见概率分布表,常用的连续概率分布汇总》的所有内容,希望对您能有所帮助!
- 最近发表